Number of Connected Components in an Undirected Graph (Java)

Given n nodes labeled from 0 to n – 1 and a list of undirected edges (each edge is a pair of nodes), write a function to find the number of connected components in an undirected graph.

For example:

     0          3
     |          |
     1 --- 2    4

Given n = 5 and edges = [[0, 1], [1, 2], [3, 4]], return 2.

Java Solution – Union-find

This problem can be solved by using union-find beautifully. Initially, there are n nodes. The nodes that are involved in each edge are merged.

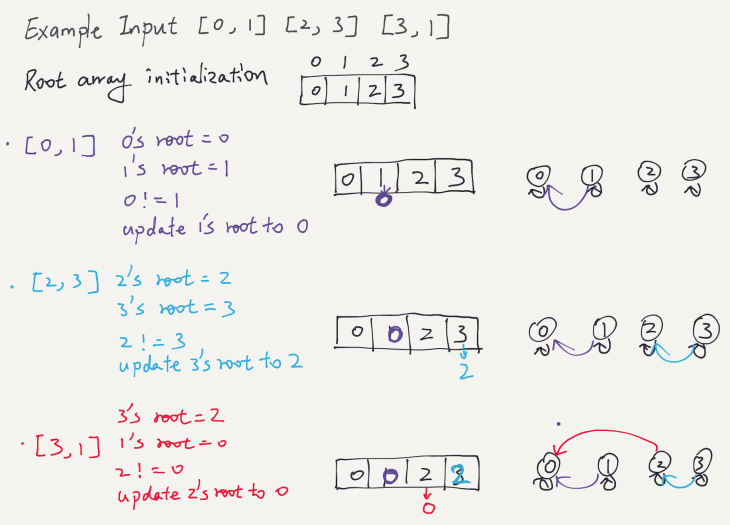
public int countComponents(int n, int[][] edges) {
    int count = n;
 
    int[] root = new int[n];
    // initialize each node is an island
    for(int i=0; i<n; i++){
        root[i]=i;        
    }
 
    for(int i=0; i<edges.length; i++){
        int x = edges[i][0];
        int y = edges[i][1];
 
        int xRoot = getRoot(root, x);
        int yRoot = getRoot(root, y);
 
        if(xRoot!=yRoot){
            count--;
            root[xRoot]=yRoot;
        }
 
    }
 
    return count;
}
 
public int getRoot(int[] arr, int i){
    while(arr[i]!=i){
        arr[i]= arr[arr[i]];
        i=arr[i];
    }
    return i;
}

There are k loops and each loop processing the root array costs log(n). Therefore, the time complexity is O(k*log(n)).